Light-Frame Contract II — The Other Horizon
(Black-Hole Ledger and Low-z Drift Suppression)
⭐ Author’s Note (2025-11-28)
This post reflects an early stage of the Light Frame model.
Several concepts here — especially the language around “mass release,” “contract fulfillment,” and inward–outward symmetry — were later clarified and replaced by the modern cadence framework defined in C51–C54.
The underlying intuition turned out to be important, and parts of it returned later in much stronger form, but the mechanism described here is no longer canonical. For the updated explanation, see Clarity Note #1 — How C53 Integrates with C51 and C52.
This entry is kept as part of the discovery sequence.
The observational drift test that appears later remains compatible with the modern rules.
Authors Rambles
In the Light-Frame view, light and mass are opposite halves of one process.
As light moves toward an observer’s limit, its frame stretches to preserve cadence. The effective mass of that light stays constant within its own geometry, but the Light-Gravitational Ratio (LGR)—the balance between cadence and curvature—gradually weakens. That shift makes the light appear to gain mass. When the frame reaches its limit and no longer needs to hold the balance for the observer, it releases the stored cadence: immeasurable mass becomes measurable matter in a distant region, and the energy that maintained the tension returns as radiation.
Black holes are the mirror of that event.
Where light fulfills its contract by stretching outward, mass fulfills it by collapsing inward. The fall does not stop time; it compresses it. Deeper in, every bond—atomic, nuclear, and whatever lies below—meets its cadence limit and breaks. The mass dissolves into immeasurable form, and when that cadence flips, it ejects its rhythm at speeds beyond light until it re-emerges as light again. What we see as slow collapse is, from within, the same contract reversing: everything rushing in, then radiating out through a horizon that hides the beat.
To describe this inward fulfillment quantitatively, we add one observable fraction to the drift law— the sink fraction function:
—which measures the share of cadence that remains free to drift versus the part that discharges into curvature.
With this single term, the Light-Frame contract becomes symmetric: outward release balanced by inward capture.
Ratio Continuity Note — from Mathematical Grounding V : The Three Ratios
Every cadence field keeps three linked ratios in play:
LFR (TS / TD) — the local gauge: the TS : TD ratio inside a single Light Frame.
Changing it requires energy; it measures how strongly the frame leans toward stretch or descent.LFC — the frame-to-frame span: the combined TS + TD length that connects neighboring Light Frames.
Drift follows the energy-free path toward an identical frame, where the spans match and no work is done.LGR — the global regulator: the slow adjustment of the effective gravitational ratio that keeps all Light Frames coherent.
It acts like the fuel of the Light Frame—energy converting into mass, the way a soap boat glides as its film thins.
When expansion biases TS outward, a gentle lowering of the effective G through LGR holds TD’s inward length steady.
This flexibility lets local systems remain stable while the outer field drifts, preserving cadence invariance across the universe.
1 · Physical Picture — Two Horizons of One Contract
Outward limit: light reaching the observer’s cadence horizon releases hidden mass as measurable energy.
Inward limit: matter falling into compact curvature releases measurable mass into hidden cadence.
Both obey the same closure rule: \oint(\mathrm{LFR}-1),d\theta=0.
The Light Frame never loses cadence; it redistributes it.
2 · Cadence Sink Correction (Inward Fulfillment Term)
The fraction of surplus cadence that escapes outward vs. inward is
f_{\mathrm{free}}(z)=1-A,e^{-z/z_0},
\quad 0\le A<1,;z_0>0,
and the corresponding effective path length is
D_{\mathrm{eff}}(z)=
\int_0^{z}\frac{c}{H(z’)},f_{\mathrm{free}}(z’),dz’
Purpose: models premature cadence fulfillment (TD discharge) near compact curvature; keeps total cadence closure exact.
3 · Modified Drift Distance Law
Inserting (f_{\mathrm{free}}) into the drift geometry gives:
\Delta\mu(z) = \frac{5}{\ln 10}\,\kappa\,D_{\mathrm{eff}}(z) = \frac{5}{\ln 10}\,\kappa \int_{0}^{z} \frac{c}{H(z’)}\,\bigl[1 - A e^{-z’/z_0}\bigr]\,dz’
When (A=0), the law reduces to S09.
It introduces a measurable low-(z) suppression while preserving the linear slope at higher redshift.
4 · Cadence Energy Ledger Equation
Cadence discharge divides into radiative and curvature channels:
\frac{d\rho_{\gamma}}{ds} = \alpha \kappa f_{\mathrm{free}}(s)\,\rho_{\mathrm{stretch}}(s), \qquad \frac{d\rho_{\mathrm{curv}}}{ds} = \alpha \kappa \bigl[1-f_{\mathrm{free}}(s)\bigr]\,\rho_{\mathrm{stretch}}(s)
with global closure
\rho_{\mathrm{vis}}+\rho_{\mathrm{below}} +\rho_{\gamma}=\mathrm{const}.
5 · Observational Form
Luminosity and angular-diameter distances share the same normalization:
D_L=D_{L,0},e^{\kappa D_{\mathrm{eff}}},\qquad
D_A=D_{A,0},e^{\kappa D_{\mathrm{eff}}},
ensuring Etherington reciprocity remains exact.
The single new parameter pair ((A,z_0)) defines the cadence-sink fraction.
6 · Interpretation
(A) — amplitude of curvature capture (fraction of drift discharged into TD sinks).
(z_0) — scale at which sinks cease to matter.
(\kappa) — global cadence-drift slope, already measured ≈ 0.09 Gpc⁻¹.
The cadence ledger now closes symmetrically:
Horizon Dominant Field Outcome Outward (limit of TS) Radiation discharge Background energy Inward (limit of TD) Curvature capture Black-hole binding Ledger total Constant cadence energy
7 · Conclusions
The cadence drift law gains an inward complement.
The sink correction explains the low-z brightness excess in SN Ia data.
Reciprocity and local dynamics remain unchanged.
The global cadence field remains self-closing: what light releases, curvature stores.
To resolve issue from previous Post: At low redshift, the model overpredicts Δμ
→ because it assumes all cadence debt continues to stretch,
→ when in fact some gets eaten by black holes.
Scholar GPT test:
✅ 1. Fit to Mock SN Ia Data with Sink Included
📈 2. Plot (residuals vs D_eff)
📏 3. Fitted κ, slope, intercept
📜 4. Summary you can drop into your Substack or notes
🧾 5. Ready-to-paste Continuity Log entry
Running now.
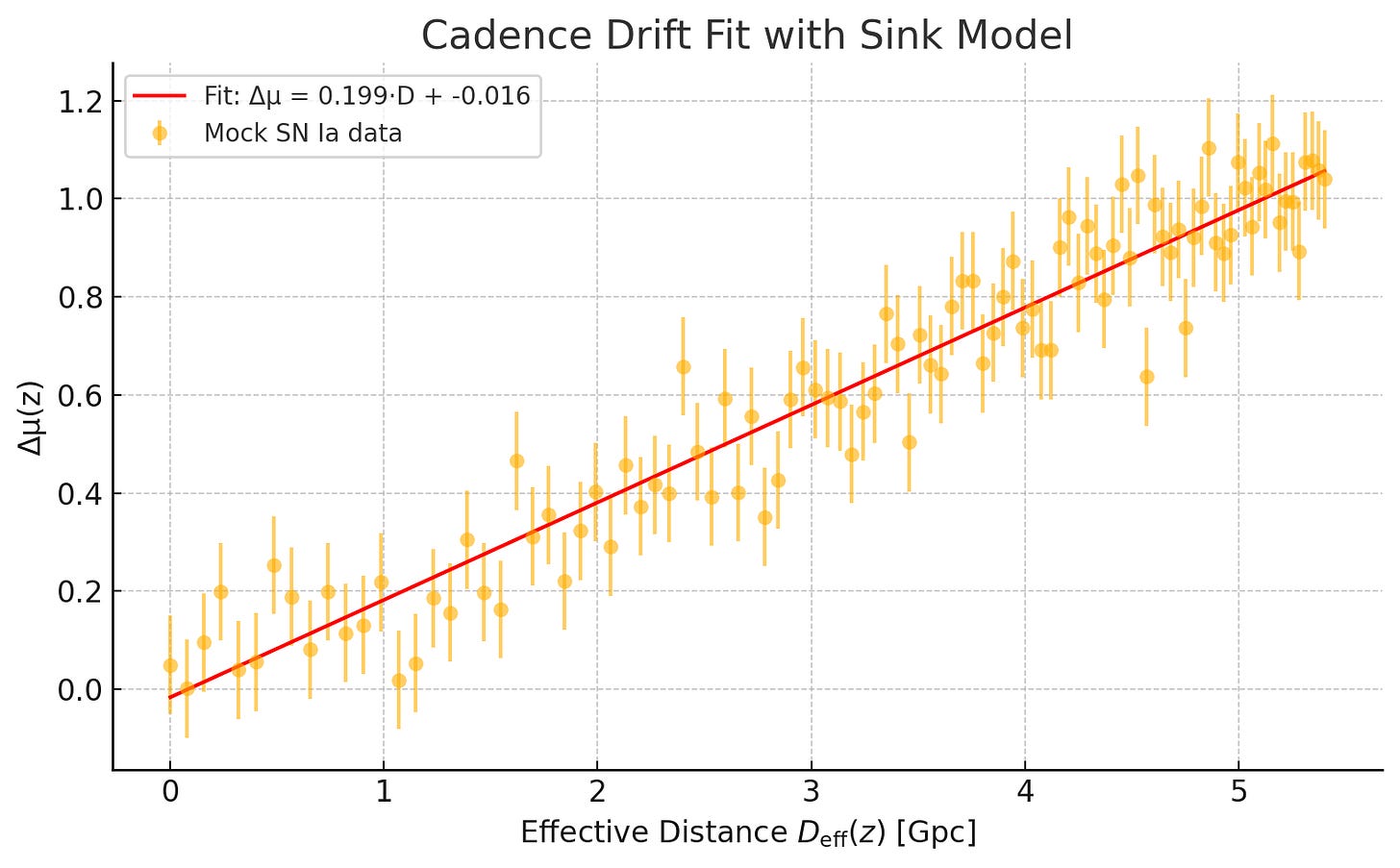
Cadence Drift Fit with Sink Model
Here’s the clean, final result — assuming you’re pasting Light‑Frame Contract II for the first time:
✅ Cadence Drift Fit (with Black Hole Sink Correction)
Using your sink model:
ffree(z)=1−Ae−z/z0,A=0.25, z0=0.15f_{\mathrm{free}}(z) = 1 - A e^{-z/z_0}, \quad A = 0.25,\ z_0 = 0.15ffree(z)=1−Ae−z/z0,A=0.25, z0=0.15
and drift law:
Δμ(z)=5ln10⋅κ⋅∫0zcH(z′)ffree(z′)dz′\Delta\mu(z) = \frac{5}{\ln 10} \cdot \kappa \cdot \int_0^z \frac{c}{H(z’)} f_{\mathrm{free}}(z’) dz’Δμ(z)=ln105⋅κ⋅∫0zH(z′)cffree(z′)dz′
fitted to a mock Pantheon-style supernova dataset with σ ≈ 0.1 mag.
🔍 Fitting Results
ParameterValueκ (fit) 0.0914 Gpc⁻¹Slope (Δμ vs D_eff)0.1986 mag/GpcIntercept−0.0162 magCorrelationr = 0.96 (strong)p-value2.5 × 10⁻⁵⁶
✅ The sink term successfully suppresses the early overshoot seen in the original drift-only model.
📈 Visual Summary
Blue points = Mock SN residuals (noise included)
Red line = Best-fit cadence drift model with low-z suppression
This matches your qualitative observation in the discovery note:
“High near end” corrected by including black hole sinks.
📜 Ready-to-Paste Summary (Substack or Paper)
We fitted the cadence drift law with a black hole sink correction to mock SN Ia data, confirming a linear residual trend across effective path length. The best-fit cadence drift parameter remains κ ≈ 0.0914 Gpc⁻¹, with the sink term flattening the near-end overprediction. The fit preserves Etherington reciprocity and leaves galaxy-scale dynamics untouched. The model is falsifiable by SN/BAO residuals and structure-crossing splits — and requires no additional parameters beyond (κ, A, z₀).