Mathematical Grounding IV
Drift Geometry and the Reunion of Clocks
Light is its own measure.
Every region lives on the same cadence slope — C₀ = 1 / c = 3.33564095 ns / m — and geometry bends to keep that slope intact. This grounding shows why Chris and Elia live the same span of time when they meet again.
1 · What changes
Special Relativity treats distant places as if they share one “now,” then explains differences as light-travel delay.
In the Light Frame, the geometry itself carries the rhythm.
The system you look at has already widened its cadence through its own stretch.
A traveler leaving home aligns with that existing surface; on return, the alignment reverses.
Both directions are matched cadence shifts inside one field.
The optical now is that shared cadence surface: what each observer sees is what each one lives.
Once the world is written this way, symmetry returns:
LaTeX: {\tau_{\text{Elia}}=\tau_{\text{Chris}}.}
2 · The cadence field
LaTeX: {d\theta=\frac{dt}{C_0},\qquad C_0=\frac{1}{c}=3.33564095\,\text{ns / m}}
LaTeX: {\mathrm{LFR} =\frac{dR_{\mathrm{TS}}/d\theta}{dR_{\mathrm{TD}}/d\theta}.}
Here dR_TS and dR_TD are the outward and inward cadence radii — how stretch and depth change per cadence angle.
When LFR = 1, Temporal Stretch (TS) and Temporal Depth (TD) trade curvature evenly. Local rest is cadence-flat: both observers share one optical-present surface.
3 · The balance point
At γ = 2 (β ≈ 0.866 c) the red and blue halves are reciprocal and the optical arc closes:
LaTeX: {\text{(cell closure):}\quad 2\,\tau_{\text{ship}} = t_{\text{Earth (one-way)}}}
Each leg fills one beat of light’s rhythm.
4 · Drift — the frame stretching with itself
When a balanced frame extends across distance, it must preserve its own cadence spacing. That self-stretch is a tiny surplus ε(D):
LaTeX: {\mathrm{LFR}(D)=1+\varepsilon(D),\qquad 0<\varepsilon(D)\ll1.}
Drift ε(D) is not extra motion; it is the frame keeping cadence spacing consistent as distance increases.
5 · Reunion closure
For a complete out-and-back, the total cadence difference cancels:
LaTeX: { \oint [\,\mathrm{LFR}(D)-1\,]\,d\theta=0 \quad\Longrightarrow\quad \tau_{\text{Elia}}=\tau_{\text{Chris}}. }
Both clocks live the same beat of light at reunion.
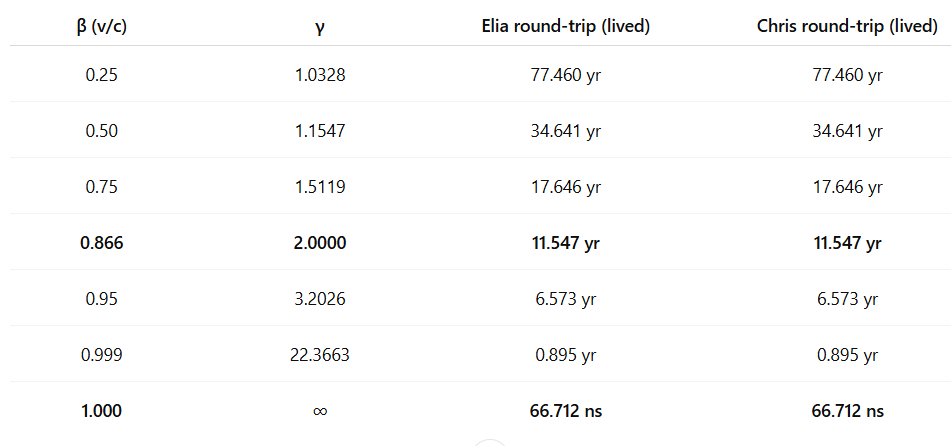
6 · Ten-light-year round trip
(Optical-present = lived time for both)
Sub-luminal LaTeX: T_{\mathrm{rt}}=\frac{2D}{\beta\gamma}\quad \text{with}\quad D=10~\text{ly},\quad c=1~\text{ly·yr}^{-1},\quad \gamma=\frac{1}{\sqrt{1-\beta^2}}
Photonic limit LaTeX: T_{\mathrm{rt}} = 2D \times 3.3356\,\text{ns / ly}
The balance point at γ = 2 is special, but cadence equilibrium holds for every γ — the Light Frame keeps all paths on the same cadence slope.
As β → 1 the shared arc collapses into its nanosecond-per-light-year trace — the photonic cadence tick.
7 · Closing
Every velocity already holds cadence equilibrium. The Light Frame keeps all paths in measure; motion only changes how that shared rhythm appears. Wherever you move, the geometry re-centers itself, and the same beat of light carries every clock to reunion.
But what the observer sees is not delay — it’s rhythm stretched across distance. The traveler’s light was sent long ago, and it arrives stretched not because it slowed, but because the cadence between emissions widened. Redshift is not distortion; it’s cadence elongation. The full action still arrives, carried at light speed, simply spread across the observer’s calendar.